같은 공간? 다른 공간?

창의력 쑥쑥 퀴즈 /

뫼비우스의 띠는 공간의 모양과 연결을 이해하기 위해 독일의 수학자이자 천문학자인 아우구스트 뫼비우스가 고안한 것이다. 긴 종이 띠의 양끝을 바로 이어서 붙인 것과 한번 꼬아서 연결한 것은 띠가 만드는 공간의 연결성이 다르다(그림1). 띠 위의 한 점에서 시작하여 계속 선을 그어 나가면 그냥 이어 붙인 고리와는 달리 모든 면에 선을 긋고 처음 점으로 돌아올 수 있다. 두 고리는 공간의 연결 상태가 달라 위상이 다르다고 한다.

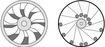
위상 문제는 공간에서 얼마나 멀리 떨어져 있는가, 얼마나 큰가를 고민하는 것이 아니다. 각이 있는가, 직선인가, 곡선인가도 중요하지 않다. 대신 공간이 어떻게 연결되어 있는가, 휘기, 누르기, 비틀기 등과 같은 연속적인 변환에 의해서 어떻게 변화하는가 하는 것이 중요하다. 위상을 기준으로 이야기 하면 삼각형이나 사각형이나 같은 것이고 도너스나 손잡이가 있는 컵이 같은 것이다. 위상을 왜 중요하게 생각해야 할까? 오일러가 풀어낸 ‘쾨니히스베르크 다리’ 문제도 기하학과 관계가 없고 다리를 연결하는 방법이었다. 지하철 지도를 만드는 것도 생각해 보면 어떤 역이 어디에 있고 역끼리 얼마나 떨어져있는가는 중요한 정보가 아니다. 역들이 어떻게 연결되어 있고 어디서 갈아타는가 하는 것이 중요한 정보인데 이것을 다루는 것이 바로 위상의 문제이다. 위상을 잘 다루어 복잡한 통신망 분석과 컴퓨터 회로 설계를 하는 네트워크 이론이 만들어졌다. 그림2의 두 가지는 고리는 위상이 같을까, 다를까?

문미옥/이화여대 와이즈거점센터(wise,or.kr) 연구교수

---

(지난주 정답)

일정한 패턴이 주기적으로 정확하게 반복되는 공간 채우기를 ‘주기적 타일링’이라고 한다. 문제에서 주어진 것과 같이 얼듯 보면 주기적인 성질이 보이는 것 같은데 자세히 따져 보면 완벽하게 정확하지 않은 주기성을 보여주는 패턴으로 채워진 것을 ‘준(準)주기적 타일링’이라고 한다. 공간 채우기 또는 공간 구성하기의 생각은 물질이 이루는 기하학적 구조를 이해하는 데도 큰 도움이 된다. 이 세상에 있는 원자가 단위가 되는 특별한 조합과 형태를 가지고 분자를 이루어 고유한 성질을 가지는 물질이 된다. 단위분자가 주기적으로 반복되어 만들어진 물질을 결정이라 한다. 준결정(quasi-crystal) 물질은 완벽하게 반복적인지 않고 규칙적인 것처럼 보이는 준주기적 배열을 가지고 있다. 준결정 물질은 금속합금으로 많이 만들어지는데 강도가 세고 잘 부식되지 않으며 결정성 물질에 비해 마찰이 낮아서 닳아지는 비율이 낮다. 준결정 물질은 항공분야나 자동차, 특수기계, 조선, 건설 등의 분야에서 기존의 재료가 가지는 한계를 극복하기 위한 맞춤식 재료로 많이 활용되고 있다.