복잡한 문제 풀이 ‘단순화’가 열쇠

수학으로 생각하고 문제 해결하기

창의적 문제해결능력

수학으로 생각하고 문제 해결하기/

8. 문제해결전략 ①
9. 문제해결전략 ②
10. 추론하기

수학 문제를 해결하려 할 때 가장 중요한 것은 문제 해결의 전반적인 절차나 해결 방법의 단서를 찾아 그것을 구체화하는 것이다. 하지만 기본적인 방법이나 수학적 지식을 알고 있어도 문제가 너무 복잡해 보이면 해결 방법을 찾기란 생각만큼 쉽지 않다.

만약 다음과 같은 질문을 받았다면 어떻게 문제풀이를 시작할 수 있을까?

문제

창의는 흰 종이에 1부터 500까지의 수를 차례대로 적으려고 합니다. 창의는 숫자 5를 모두 몇 번 적게 되는지 구하시오.

1, 2, 3, 4, 5, 6, 7, … 500

일단 500까지 실제로 써보는 방법이 있을 수 있지만 너무 번거로운 일이다. 좀더 효율적인 방법을 찾아보자. 복잡한 문제일수록 문제를 몇 개의 부분으로 나누어 생각해 보거나 단순화해 보면 의외로 간단하게 해결책을 찾을 수 있다. 이런 문제해결 전략을 ‘단순화해 해결하기 전략’이라고 한다.

‘단순화해 해결하기 전략’은 문제에 제시된 수가 크거나 계산이 복잡할 경우 이를 간단한 수로 고치거나 좀더 단순한 문제로 고쳐서 해결해 보고, 해결 과정을 원래 문제에 적용함으로써 문제를 쉽게 푸는 방법이다. 또 원래의 문제를 몇 개의 부분적인 문제로 나누어 그들을 해결함으로써 본 문제를 쉽게 푸는 방법이기도 하다. 이 전략은 ‘규칙성을 찾아 해결하기’, ‘표 만들어 해결하기’ 등의 전략과도 관련이 깊으며 다른 전략의 보조적인 구실을 하는 중요한 전략이라고 할 수 있다.

그럼 예시 문항을 ‘단순화해 해결하기’ 전략으로 풀어보자.

1. 이 문제는 1부터 500까지의 숫자를 차례대로 쓰는데 5를 모두 몇 번 적게 되는 것인지를 구해야 한다.

2. 문제를 해결하기 위해 일의 자리, 십의 자리, 백의 자리로 나누어 숫자 5가 몇 번 사용되는지 찾아보자.

3. 먼저 일의 자리를 생각해 보자. 1부터 9까지는 5가 1번 들어가게 되며, 10부터 19까지도 5는 1번 쓰게 된다. 마찬가지 방법으로 나머지도 구하여 표로 정리하면 다음과 같다.

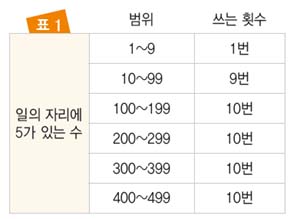4. 일의 자리와 마찬가지로 십의 자리, 백의 자리도 구해보자.

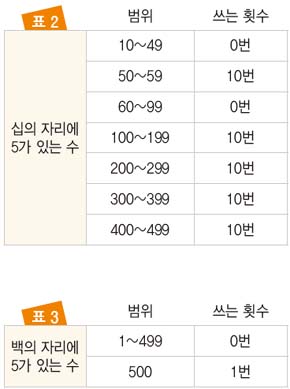5. 이제 구한 개수를 모두 더하면 풀이를 완성할 수 있다. 일의 자리, 십의 자리, 백의 자리를 더한 값은 101이기 때문에 창의는 1부터 500까지의 수를 쓰는 데 5를 모두 101번 쓰게 된다.
이처럼 복잡한 문제나 문제해결 전략이 잘 보이지 않는 문제를 접했을 때는 일단 문제를 단순화하면 좀더 효과적인 풀이법을 찾을 수 있다.
단순화하는 방법은 위에서도 말했듯이 원래 문제를 간단한 수로 고쳐 단순화할 수도 있고, 문제에서 제시된 범위를 나누어 보거나 문제를 여러 개의 문제로 나누어 단순화할 수도 있다.
이것은 문제의 상황마다 다르게 적용되므로 여러 가지 문제를 단순화하는 연습을 통해 적용력을 기르도록 하자.
특히 ‘단순화해 해결하기 전략’은 복잡한 계산이 포함된 문제, 아주 큰 수나 아주 작은 수가 포함된 문제, 연속된 수의 합을 구하는 문제, 직접적인 풀이가 매우 복잡한 문제 등의 문제를 푸는 데 효과적이다.

김은경 연구원 와이즈만 영재교육연구소

생각해보자

한 변의 길이가 800m인 정사각형 모양의 호수 둘레에 2m 간격으로 나무를 심으려고 한다. 나무는 모두 몇 그루가 필요한지 구하시오.

▶ 풀이는 <아하 한겨레> 누리집(www.ahahan.co.kr)의 ‘교육정보’면에서 확인하세요.

김은경 연구원 와이즈만 영재교육연구소