3차원 공간에 밀도있게 공을 쌓는다면…

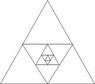
창의력 쑥쑥 퀴즈 /

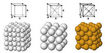
1611년에 행성의 운동을 관찰해 법칙을 알아낸 케플러는 과일가게에서 사과를 쌓아 올리는 방법이, 같은 크기의 공을 쌓아갈 때 공간을 가장 빽빽하게 채우면서 쌓는 방법이라고 추측했다. 이 방법이나, 면심입방 구조나 육모꼴에 모두 같은 크기의 공을 쌓는 경우 공간을 차지하는 비율이 약 74%로 같다. 공이 공간을 최대한 차지하도록 하려면 공과 공이 마주 닿도록 붙여나가야 할 것이다. 직선으로 공을 연결한다면 공 한개에 이웃해 맞붙는 공의 수가 2개가 되고 평면에서는 그림처럼 공 6개가 주변에서 맞붙어 꽉 차야 한다. 3차원 공간에서 가장 밀도 있게 공을 쌓는다면 맞붙는 공의 수는 몇 개일까?

문미옥/이화여대 와이즈거점센터(wise.or.kr) 연구교수

---

지난주 정답

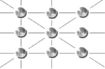
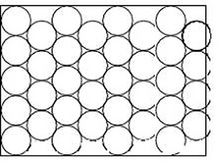35개의 푸딩이 꽉 찬 케이크 상자에 1개 더 넣으려면…. 수학적으로는 불가능하다. 그림처럼 푸딩을 엇갈리게 놓으면 푸딩이 차지하고 남은 공간을 조금씩 더 활용해서 옆으로 5개씩 7줄이던 것(이때는 상자를 78% 정도 활용한다)을 5개씩 4줄 사이에 4개씩 4줄을 더 만들면(이때는 상자를 90%정도 활용한다) 푸딩을 1개 더 넣을 수 있을 것 같지만 아주 약간 자리가 모자란다(푸딩의 반지름이 5cm였다면 0.6cm 정도 모자란다). 그러나 현실적으로는 케이크 상자가 딱딱한 나무로 만들어져서 움직일 수 없다면 푸딩을 조금 빽빽하게 밀어야 하고, 상자가 종이로 만들어졌다면 상자를 약간 벌리고 살살 넣으면 된다. 수학에서는 약간의 차이를 허용하지 않지만 기술에서는 현실적 가능성의 여유가 있다.